
#WORD PROBLEMS CALCULUS CHAIN RULE FULL#
We know that the cone is full of water, but the water is draining. To differentiate h(x)f(g(x)) h ( x ) f ( g ( x ) ), begin by identifying f(x) f ( x ) and g(x) g ( x ).
#WORD PROBLEMS CALCULUS CHAIN RULE FREE#
At what rate is the water draining from the cone? Math Hints: Easy Mathematical Tricks from Counting Through Calculus (formerly ) is a free website that includes hundreds of pages of math, explained in simple terms, with thousands of examples of worked-out problems. Problem-Solving Strategy: Applying the Chain Rule.

Initially it is full of water, but the water level falls at a constant rate of 1cm per second. Question 1: A cone is 30 cm tall, and has a radius of 5 cm. Category Excellent Very Satisfactory Needs Satisfactory Improvement Content- Output has no Output has 1- Output has 4- Output has Accuracy errors. You may select the number of problems, and the notation. The student will be given composite functions and will be asked to differentiate them using the chain rule. Your work will be graded according to the given rubrics. These Calculus Worksheets will produce problems that involve using the chain rule to differentiate functions. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright. Let's take a look at a related rates cone problem. Make your own Chain Create three-word problems featuring the application of Chain Rule. Home > Word Problems calculators > Unitary Method (Chain Rule) calculator. Let's take a look at a few Calculus practice problems using these steps. Unitary Method (Chain Rule) calculator - Direct proportion : Which is the best.

Substitute the given information into the differential equation and solve for the asking rate. Write an equation that relates the various quantities of the problem.ĥ.ĝifferentiate both sides of the equation, with respect to time, using the Chain rule.Ħ. If possible, draw a diagram to help visualize the problem.Ģ.Ğxpress the given information and rates (look for units with time in the denominator)ģ.Ğxpress the asking rate (look for phrases such as "how fast", "at what", "find the rate", etc).Ĥ. Finding the derivative of the outside function may be a bit trickier because it also calls for the chain rule. First, let’s find the derivative of the inside function. Here are the following steps in solving a related rates question:ġ. For this problem: 5x-2 is our inside equation (g(x)). However once you know these 6 steps, then you should be able to solve any Calculus related rates problems you like.
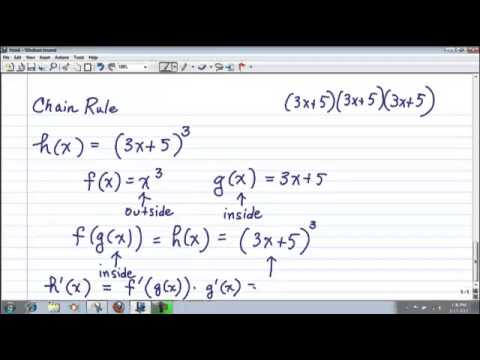
This is because each application question has a different approach in solving the problem, and requires the application of derivatives. One of the hardest calculus problems that students have trouble with are related rates problems.


 0 kommentar(er)
0 kommentar(er)
